이미지 인식에서 널리 사용되는 네트워크
convolution, pooling layer → feature extraction
fully-connected layer → classification
Convolution
Convolution filters
- 필터의 특징이 연산되어 이미지 변형(엠보싱, 엣지, 블러, 샤프닝 등)
- 딥러닝에서는 특징을 찾아낼 필터를 알아서 학습해서 사용
CNN 동작원리
- 필터를 이동시켜 특징을 찾음
- 특징에 대한 점수표가 나옴
- 다음 layer로 갈수록 더 크게 확장해서 봄
2D Convolutional Layer
- channel (depth)
- height, width : filter의 크기
- stride : filter이 이동거리
- input의 채널 수와 filter의 채널 수는 같아야 함

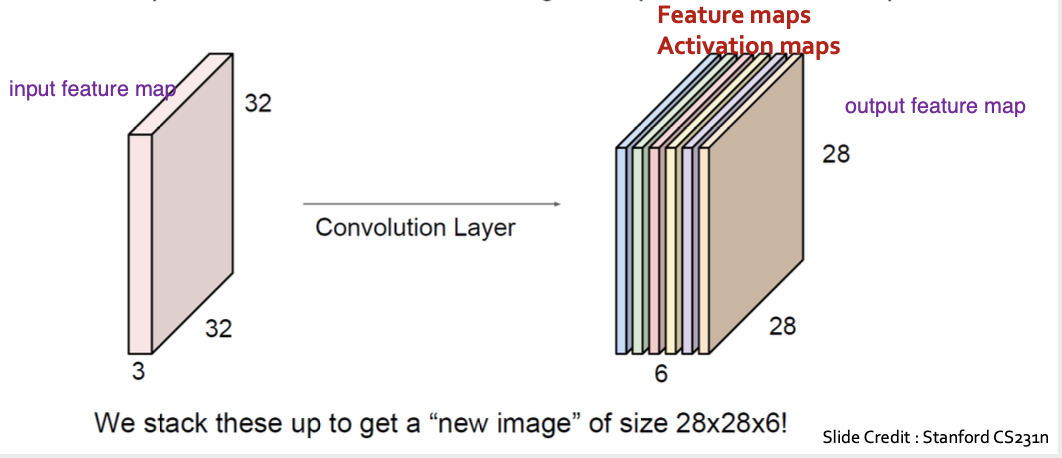
- 필터를 6개 사용할 경우feature map은 6개
- output 채널수는 사용한 filter의 개수와 같음
Dense Layer vs 1-D Convolution Layer

1-D connolution layer 특징
- weight 공유 (sharing, sliding)
- locally connected
- 데이터의 일부만 사용(local 영역)하고, weight를 reuse (dense layer에서는 weight가 한번만 계산에 사용)
computation

input image: 3차원, filter: 4차원, feature map: 3차원
실제로는 batch 단위로 학습하기 때문에 전부 4차원 tensor로 구성
Options of Convolution
- stride: filter가 옆/아래로 몇 칸씩 이동할 것인가? (각각 다르게 설정 가능)
- zero padding: 입력과 출력의 값을 동일하게 만들어 주기 위해 이미지 주변에 zero을 채워주는 계산 (why 0? 연산에 영향을 주지 않음)
Pooling
Pooling Layer
- ilter 영역 내에서 max, average값을 구함
- 출력 크기를 줄임
- 채널별로 하므로 풀링 후 채널 수 바뀌지 않음
- 학습은 없음 → 파라미터가 없음
- Max pooling 더 많이 사용 (점수가 높은 부분을 살려서 가져가는 것)
- location invariant : 공간적 위치 변화에 invariant (치우쳐 있어도 중요 특징 추출)
Fully-Connected Layer
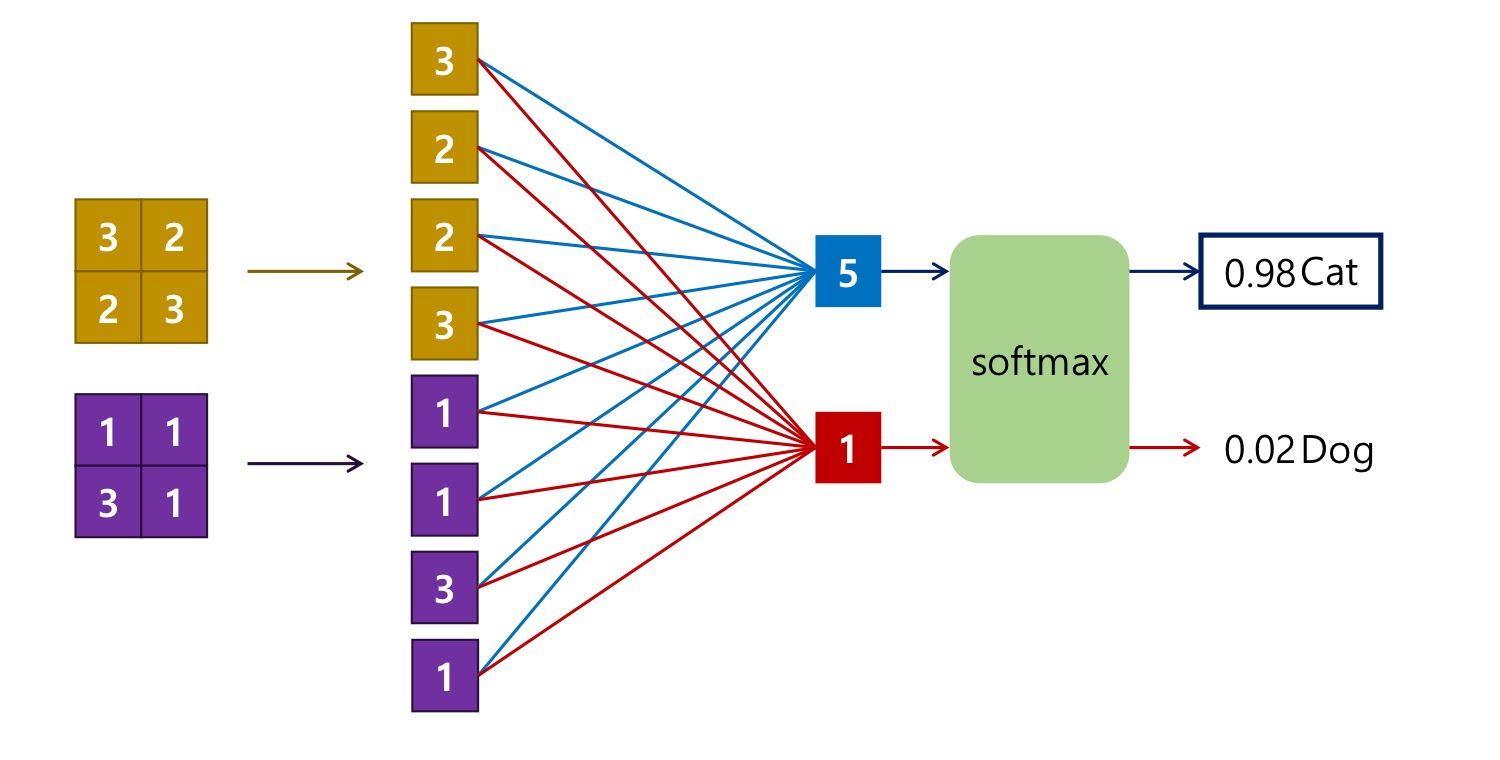
- 마지막에 flatten으로 일렬로 쭉 펴서 dense layer에 집어 넣음
- Convolution Layer에서 뽑은 특징으로 Image 분류
고전적 CNN의 특징
- local invariance에 강하고 rotation에 대해 취약
- rotation invariance가 필요할 경우 회전된 이미지를 augmentation해서 학습
- 파라미터 수는 대부분 FC layer가 대부분
- 연산량은 convolutional layer가 대부분
- convolution layer는 weight을 share하기 때문에 연산량이 훨씬 많음
CNN의 역사

1) AlexNet (Krizhevsky, 2012)

- ReLU, norm layer, Dropout 사용
- Data Augmentation
- GPU 성능 때문에 데이터 두개로 나누어서 처리 (후에 한번에 처리하는 것보다 성능 좋음)
- [Conv1 – Pool1 – Norm1 – Conv2 – Pool2 – Norm2 – Conv3 – Conv4 – Conv5 – Pool 5 – FC6 – FC7 – FC8]
2) ZFNet (Zeiler and Fergus, 2013)

- AlexNet와 비슷
- stride 4 -> 7x7 stride 2
- conv 3, 4, 5 : 필터의 개수 384, 384, 256 -> 512, 1024, 512 사용
3) VGGNet (Simonyan and Zisserman, 2014)
- Deep Learning 구조 틀의 기본이 되는 네트워크
- layer가 지날수록 이미지 크기 감소, channel 수 증가
- 3x3 filter의 stride 1 convolution만 사용
- 동일한 reception field에 적은 파라미터 사용 가능
- non-linearity 증가
- 파라미터가 많고, 연산량이 많음 (치명적 단점)
4) GoogLeNet (Szegedy, 2014)
Sparse Connectivity
- 관련성 가진 노드끼리만 연결
- computational resource를 적게 사용
- overfitting 개선
- fully connected
Inception Module

- Naive Inception Module
- 여러 크기의 커널을 사용
- 마지막에 channel 방향으로 concat
- 다양한 respective field
- layer가 쌓일수록, channel이 딥해지면서 계산량 많아짐
- 1x1 convolution
- bottle neck layer
- 이미지의 크기를 유지하면서, channel 수 감소
- 1x1 Conv을 넣어 channel을 줄였다가, 다음의 3x3, 5x5 Conv에서 다시 확장하여 필요한 연산량 감소시킴
- dense한 output 만들어냄
- H와 W는 모두 동일 (concat을 channel에 적용)
Global average pooling
- 마지막에 channel별로 average pooling
- fc을 통해 classification
- fc의 파라미터 수 줄이는 효과
Stem Network
- 레이어의 앞단으로 모든 인셉션 모듈
- Conv - Pool - 2 x Conv - Pool
Auxiliary classification
- vanish gradient 현상 발생 -> 역전파
- training시 model 중간에 auxiliary classification 추가
- 마지막 testing엔 제거

5) ResNet (He, 2015)
- 2015년 모든 ILSVRC 대회에서 우승
- layer수가 152개로 확 늘어남
- top-5 error가 3.6%로 사람의 능력 (5%) 뛰어넘음
degradation
- 과적합과는 다른 훈련용 데이터에 대한 성능 문제
- layer가 늘어날수록, 모델의 성능이 줄어드는 현상 발생
skip connection
- F(x) = H(x) - x ; 잔차를 학습
- 출력 H(x) = F(x) + x
- 네트워크의 입력과 출력이 더해진 것을 다음 레이어의 입력으로 사용
- 최적의 경우 F(x)=0인 학습 목표가 정해져 있으므로 속도가 빠르고 작은 변화에도 민감하게 반응
- 이전 스텝의 그래디언트(정보)를 좀 더 잘 흐르게 만들려는 long term short memory(LSTM)의 철학과 유사

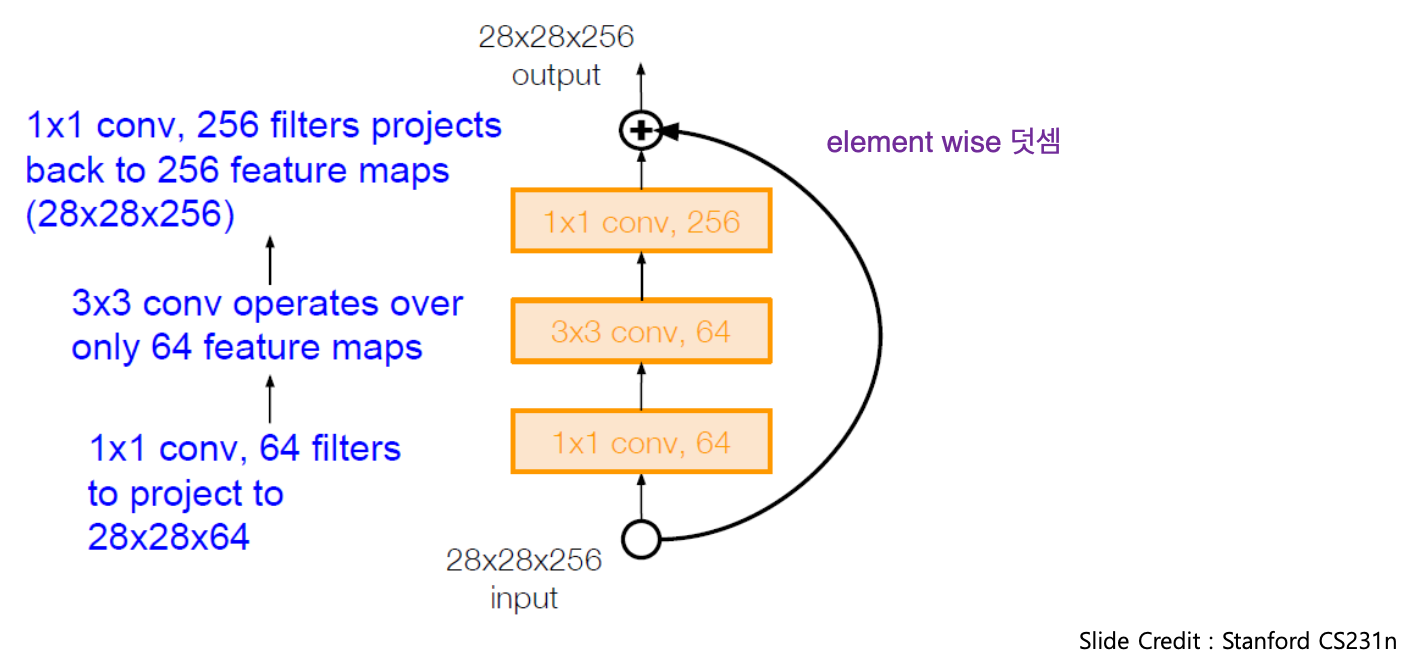
bottle neck layer
연산량을 줄이기 위해 Residual block 내에 1x1, 3x3, 1x1 conv 연산 추가
'DEEP LEARNING > Fundamental Concept' 카테고리의 다른 글
| Object Detection (0) | 2020.03.25 |
|---|---|
| Modern CNN (0) | 2020.03.10 |
| Training Neural Networks (0) | 2020.02.24 |
| Linear Regression & Logistic Regression (0) | 2020.02.12 |
| What is AI? (0) | 2020.02.02 |



